Examples

  1. Home
  2. Examples

Forwarders

Simple forwarder
A one-hop forwarder from channel a to channel b that can be written as . Its persistent version is .

Alternating forwarder
An alternating forwarder A(a,b,c) from channel a to channel b first and then to channel c can be defined as .

Non deterministic forwarder
A persistent non-deterministic forwarder from a to any of c1, ...,cn can be written as .

The leader election problem

This is a classical problem in distributed computing where the participants, organised in a symmetric ring, have to reach an agreement in electing a leader by running symmetric protocols. Each process is only aware of its own peers. We write

for the process that communicates on channel l on its left, on channel r on its right, and that uses channel w to declare itself to be the leader (winner). For a ring with three peers, the code specification is: .
The schema of the leader election problem with three processes is:

Whatsapp

We model the communication schema similar to the one of Whatsapp. We propose two versions: the synchronous and the asynchronous ones. In the first version either each participant to the group receives the message, or no one receives it. In the second version it is not guaranteed that all the participants to the group receives the message at the same time.

Dining philosophers

The classical problem of the dining philosophers relates n philosophers sitting around a table; each one has its own dish, and they can only eat or think. When they, independently, decide to eat, they need two forks. There is only one fork between two dishes (i.e. n forks).

The link-calculus model, for each philosopher is:

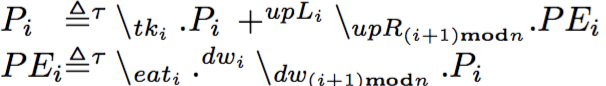
Also the forks are modeled as processes:

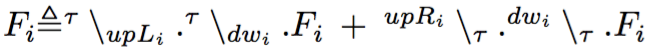
Using the multiparty interaction, the resulting abstract level is not subject to the deadlock problem. Therefore, one can focus on other properties, such as a specific fairness solution. Here there is an implementation in the link-calculus, and its labelled transition system by executing the symbolic semantics of the link-calculus.