The link-calculus homepage
"Increased expressiveness is not a theoretical luxury, but an eminently practical goal, since formal specification languages should describe as simply and naturally as possible the widest possible class of systems" -- José Meseguer
Link-calculus - without mobility - Core Network Algebra (CNA) (subsumes CCS)
Traditionally in process algebras, communication
is based on send/receive synchronisation on specific channels. In link-calculus, instead, action prefixes are given in terms of links
that record the source (input) and the target (output) ends of each hop of interactions. Links
can be combined in link chains in order to describe how information can
be routed across processes before arriving at destination. Thus, communication is inherently multiparty.
Link-calculus also allows for uncomplete interactions by the way of virtual links, i.e.
free spaces in a link-chain that can eventually accept other processes to interact with.
Link-calculus - with mobility (subsumes pi-calculus)
The interaction mechanism is the one described for CNA. Here, interactions make use
of a data tuple. Each participant can provide data or variables to be members of the data
tuple. Thus, all participants are peers, as they can send and receive data in the
same interaction.
chained Core Network Algebra (cCNA) The generalisation of link prefixes to chain prefixes is very expressive to encode some simple patterns of interaction directly in the action prefixes, thus enhancing the modelling power.
Some results
Membranes as processes
The link-calculus interaction mechanism forms link chains
composed by link prefixes. This allows us to encode membranes, or more in general
localities as processes that participate to the interaction. In fact,
membranes play an active role in the process interaction: they allow or block
the interaction depending on how processes are located.
It follows that calculi with membranes are intrinsecally multiparty. This figure shows how the movement of an ambient into another one is realized as a three-party interaction.
Bisimilarity is a congruence
Notably, bisimilarity equivalence is a congruence also w.r.t. substitutions and prefixing.
Basically, this is due to the fact that in link-calculus
these two processes:
,
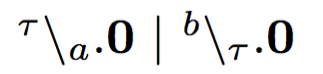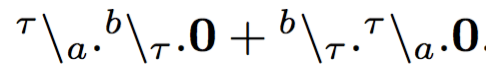
are not bisimilar,
whereas, e.g., in CCS the following holds:
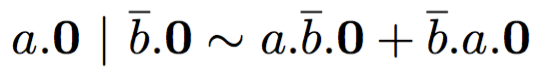but when b is replaced by a the two processes are no longer bisimilar, because the first can perform a silent action.
Rougly, we can say that link bisimulatio(without mobility) is somehow less restrictive than CCS strong bisimulation and more restrictive than CCS weak bisimulation.
Communication backbone
Thanks to the expressivity of the chained link-calculus (cCNA), it is possible to divide the processes involved in an interaction in two sets: the set of processes providing the links that define the so-called backbone of the interaction, defining the whole path to follow from end to end and the set of processes providing those solid links that fill the virtual links in the backbone.
Symbolic Link Modal Logic
The symbolic Link Modal Logic, defined on top of the symbolic semantics for the link-calculus, is a smooth extension of the Hennessy-Milner logic which is able to characterize the (symbolic) transitions of CNA processes. Moreover, similar to CCS, link bisimilar processes (without mobility) satisfy the same formulas in this logic.